跳到主要内容

一些知识

高斯分布​

高斯分布(Gaussian distribution)又名正态分布，被广泛用于表征随机变量的特征。 因为根据中心极限定理，大量独立的随机实验，趋于高斯分布。 而测量误差是独立随机的，所以认为误差的和服从高斯分布。

若随机变量 $X$ 服从一个均值为 $μ$ 、方差为 $σ$ 的正态分布，记为：

$$ X \sim N( μ , σ^2 ) $$

高斯分布图

相应的概率密度函数(PDF)为：

$$ f(x)= {\frac1{σ\sqrt{2\pi}}} e^{-{\frac{(x-μ)^2}{2σ^2}}} $$

概率密度函数的累积分布函数

若 $μ = 0$ 、 $σ = 1$ 则称为标准正态分布（均值 $μ$ 可以理解为中心线位置，方差 $σ$ 可以理解为分布的“肥胖”程度。）。

高斯混合模型示意图

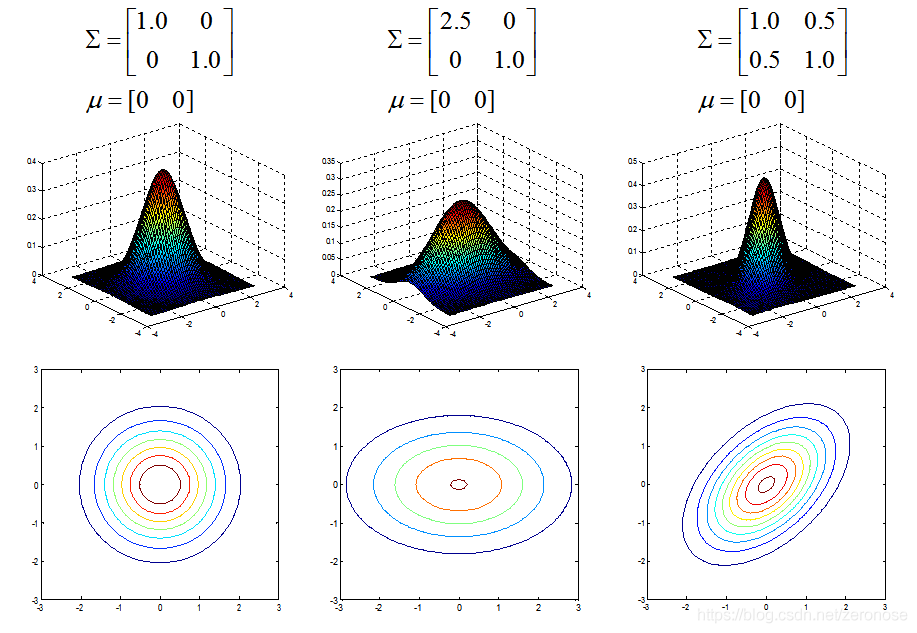
在高维空间也可以使用，故许多算法会使用这个基础原理。

一些小补充​

累计分布函数：

$$ \Phi(z)=\frac{1}{2}[1+{erf}(\frac{z-μ}{σ\sqrt{2}})] $$

误差函数：

$$ {erf}(x) = \frac{1}{\sqrt{\pi}}\int{-x}^{x} e^{-t^2} \mathrm{d}t = \frac{2}{\sqrt{\pi}} \int{0}^{x} e^{(-t^2)} \mathrm{d}t $$

互补误差函数：

$$ {erfc}(x) =1 - {erf}(x)= \frac{1}{\sqrt{2\pi}} \int_{x}^{+\infty} e^{(-t^2)} \mathrm{d}t $$

高斯分布的矩母函数（MGF）,定义为 $exp(tX)$ 的期望值：

$$

Mx(t) = E(e^{tX}) \ ~\ =\int{- \infty }^{+ \infty } \frac{1}{ \sigma \sqrt{2\pi}} e^{(- \frac{(x-\mu)^2}{2 \sigma ^2})}e^{tx} \mathrm{d}x \ ~\ = e^{ (\mu t + \frac{\sigma ^2 t^2}{2})}

$$

高斯分布的特征函数，定义为 $exp(itX)$ 的期望值：

$$ \Phi x(t; \mu , \sigma ) = E[exp(itX)] \ ~\ =\int{- \infty }^{+ \infty } \frac{1}{ \sigma \sqrt{2\pi}} exp{(- \frac{(x-\mu)^2}{2 \sigma ^2})}exp(itx) \mathrm{d}x \ ~\ = exp{ (i \mu t + \frac{\sigma ^2 t^2}{2})} $$

文中部分图片和内容来自维基百科和微信公众号收集

JavaScript 笔记​

  • 由于 JavaScript 的设计缺陷，不要使用 == 比较，始终坚持使用 === 比较。

  • 唯一能判断 NaN 的方法是通过 isNaN() 函数：

  • 在 strict 模式下运行的 JavaScript 代码，强制通过 var 申明变量，未使用 var 申明变量就使用的，将导致运行错误。